Jump to
-  Calculator
-  Definitions
Table of Contents
-  Calculator
-  Definitions
-  Geometry
Share this
See also
Sphere properties
Cone properties
Torus properties
Cylinder properties
Pyramid properties
All solids
All Geometric Shapes

Properties of Ellipsoid

- By Dr. Minas E. Lemonis, PhD - Updated: March 3, 2019
Home > Solids > Ellipsoid

This tool calculates the basic geometric properties of an ellipsoid. Enter the shape dimensions a, b and c below. The calculated results will have the same units as your input. Please use consistent units for any input.

a =
b =
c =
icon

Geometric properties:
Volume =
Surface area =
shape details

ADVERTISEMENT

Table of Contents
-  Calculator
-  Definitions
-  Geometry
Share this

Definitions

Geometry

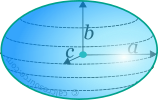
The ellipsoid is a 3-dimensional surface, the points of which, in Cartesian coordinates, satisfy the following equation:

\frac{x^2}{a^2} + \frac{y^2}{b^2} +\frac{z^2}{c^2} = 1

where a,b,c are the radii of the ellipsoid along its principal axes x, y and z respectively. It can be seen from the above formula, that ellipsoid is, in three dimensions, analogous to the ellipse in two dimensions.

The volume enclosed by an ellipsoid is given by the formula:

V = \frac{4}{3}\pi a b c

where a, b, c the three radii along the ellipsoid principal axes.

The outer surface area of the ellipsoid is not available in a closed form formula. Exact calculation requires the evaluation of elliptical integrals of the first and second kind, and is given by the equation:

A = 2\pi c^2 + \frac{2\pi a b}{\sin{\varphi}}\Big(\mathrm{E}\left(\varphi, k\right) \sin^2{\varphi} + \mathrm{F}\left(\varphi, k\right) \cos^2{\varphi} \Big)

where \mathrm{F}\,\left(\varphi, k\right) the incomplete elliptic integral of the first kind, \mathrm{E}\,\left(\varphi, k\right) the incomplete elliptic integral of the second kind and:

\begin{split} & \varphi & = \arccos{\frac{c}{a}} \\ & k & = \sqrt{\frac{a^2\left(b^2-c^2\right)}{b^2\left(a^2-c^2\right)}} \\ \end{split}\\ a \ge b \ge c\\

An approximate formula for the estimation of the surface area of the ellipsoid is:

A \approx 4\pi\left(\frac{a^p b^p + a^p c^p + b^p c^p}{3}\right)^{\frac{1}{p}}

A value of p=1.6075 yields the best approximation, with an error of the order 1%.

The calculator in this page finds the surface of the ellipsoid, using the precise formula, through numerical computation of the elliptic integrals.

See also
Sphere properties
Cone properties
Torus properties
Cylinder properties
Pyramid properties
All solids
All Geometric Shapes