Share this
See also
Moment of Inertia of a Triangle
Moment of Inertia of Trapezoid
Moment of Inertia of a Rectangle
Moment of Inertia of a Circle
Moment of Inertia of an Angle
Moment of Inertia of a I/H section
Moment of Inertia of a Rectangular tube
Moment of Inertia of a Circular tube
Moment of Inertia of a Channel
Moment of Inertia of a Tee
All Moment of Inertia tools

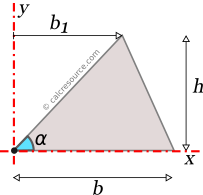
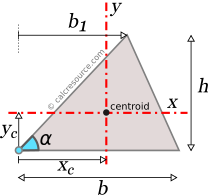
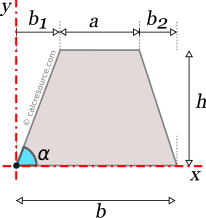
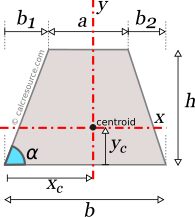
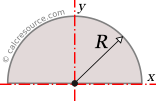
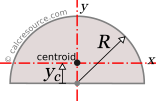
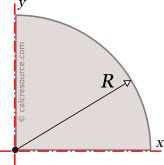
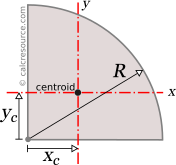
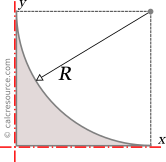
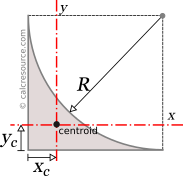
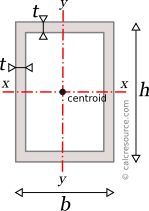
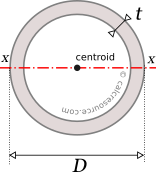
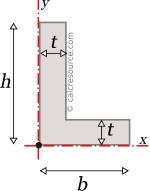
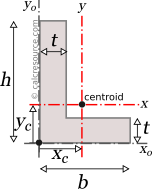
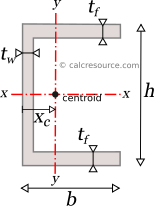
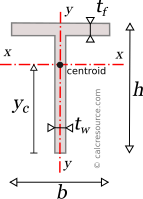
Moments of Inertia - Reference Table

- By Dr. Minas E. Lemonis, PhD - Updated: June 23, 2020
Home > Resources > Moments of Inertia Table

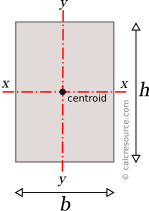
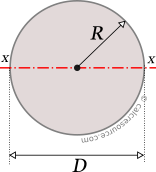
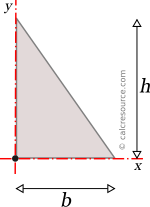
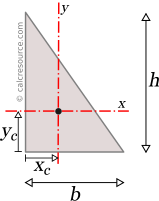
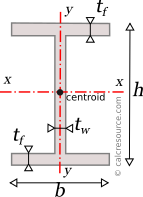
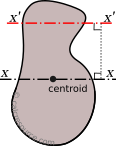
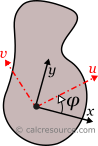
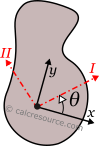
Analytical formulas for the moments of inertia (second moments of area) Ix, Iy and the products of inertia Ixy, for several common shapes are referenced in this page. The considered axes of rotation are the Cartesian x,y with origin at shape centroid and in many cases at other characteristic points of the shape as well. Also, included are the formulas for the Parallel Axes Theorem (also known as Steiner Theorem), the rotation of axes, and the principal axes. 

Table of contents

-  Rectangle | axes through centroid
-  Rectangle | axes through corner
-  Circle | any axis through center
-  Right Triangle | axes through corner
-  Right Triangle | axes through centroid
-  Triangle | axes through to corner
-  Triangle | axes through centroid
-  Trapezoid | axes through corner
-  Trapezoid | axes through centroid
-  Semicircle | axes through circle center
-  Semicircle | axes through circle centroid
-  Quarter-circle | axes through corner
-  Quarter-circle | axes through centroid
-  Quarter-circular spandrel | axes through corner
-  Quarter-circular spandrel | axes through centroid
-  Rectangular tube | axes through centroid
-  Angle | axes through corner
-  Angle | axes through centroid
-  Channel | axes through centroid
-  Tee | axes through centroid
-  Double-tee | axes through centroid
-  Parallel Axes Theorem
-  Axes rotation
-  Principal axes

Reference Table

Area Moments of Inertia

ShapeFormulae
Rectangle | axes through centroid

I_x=\frac{b h^3}{12}

I_y=\frac{h b^3}{12}

I_{xy}=0

Rectangle | axes through corner

I_x=\frac{b h^3}{3}

I_y=\frac{h b^3}{3}

I_{xy}=\frac{b^2 h^2 }{4}

Circle | any axis through center

I_x=\frac{\pi R^4}{4}=\frac{\pi D^4}{64}

Right Triangle | axes through corner

I_x=\frac{b h^3}{12}

I_y=\frac{h b^3}{12}

I_{xy}=\frac{b^2h^2}{24}

Right Triangle | axes through centroid

I_x=\frac{b h^3}{36}

I_y=\frac{h b^3}{36}

I_{xy}=-\frac{b^2h^2}{72}

Centroid:

  • y_c=h/3
  • x_c=b/3
Triangle | axes through to corner

I_x=\frac{b h^3}{12}

I_y=\frac{b h(b^2 +b b_1 +b_1^2)}{12}

I_{xy}=\frac{bh^2}{24}\left(b+2 b_1\right)

where:

  • b_1={h\over\tan{a}}, \quad a\neq 90^\circ (negative if angle a is obtuse)
Triangle | axes through centroid

I_x=\frac{b h^3}{36}

I_y=\frac{bh }{36}\left(b^2-b b_1 + b_1^2\right)

I_{xy}=-\frac{bh^2}{72}\left(b-2 b_1\right)

where:

  • y_c=h/3
  • x_c=\frac{b+b_1}{3}
  • b_1={h\over\tan{a}}, \quad a\neq 90^\circ (negative if angle a is obtuse)
Trapezoid | axes through corner

I_x=\frac{h^3\left(3 a+b\right)}{12}

I_y=h\frac{12b^3 -3b_1^3 -b_2^3 -2 b_2 (3b-b_2)^2 }{36}

I_{xy} = {h^2}\frac{3a^2+b^2 +2a b +6a b_1+2b b_1 }{24}

where:

  • b_1={h\over\tan{a}}, \quad a\neq 90^\circ (negative if angle a is obtuse)
  • b_2=b-a-b_1
Trapezoid | axes through centroid

I_x=\frac{h^3}{36}\frac{a^2+4a b + b^2}{a+b}

I_y=I_{y_0}- A x_c^2

I_{xy} = {h^2\over 72}\frac{(b_1-b_2)(a^2+4a b + b^2) }{a+b}

where:

  • I_{y_0}=h\frac{12b^3 -3b_1^3 -b_2^3 -2 b_2 (3b-b_2)^2 }{36}
  • A=h\frac{b+a}{2}
  • b_1={h\over\tan{a}}, \quad a\neq 90^\circ (negative if angle a is obtuse)
  • b_2=b-a-b_1

Centroid:

  • x_c = \frac{b^2 +a^2 + a b + 2 a b_1 + b b_1}{3(a + b)}
  • y_c=\frac{h}{3}\frac{2a+b}{a+b}
Semicircle | axes through circle center

I_x=I_y=\frac{\pi R^4}{8}

I_{xy}=0

Semicircle | axes through circle centroid

I_x=\frac{9\pi^2-64}{72\pi}R^4

I_y=\frac{\pi R^4}{8}

I_{xy}=0

Centroid:

  • y_c=\frac{4R}{3\pi}
Quarter-circle | axes through corner

I_x=I_y=\frac{\pi R^4 }{16}

I_{xy}= \frac{1}{8}R^4

Quarter-circle | axes through centroid

I_x=I_y=\frac{9\pi^2-64}{144\pi}R^4

I_{xy}=\frac{9\pi-32}{72\pi}R^4

Centroid:

  • x_c=\frac{4R}{3\pi}
  • y_c=\frac{4R}{3\pi}
Quarter-circular spandrel | axes through corner

I_x =I_y= \frac{16-5\pi}{16}R^4

I_{xy}= \frac{19-6\pi}{24}R^4

Quarter-circular spandrel | axes through centroid

I_x =I_y= \frac{9\pi^2-84\pi+176}{144(4-\pi)}R^4

I_{xy}= \frac{28-9\pi}{72(4-\pi)}R^4

Centroid:

  • x_c=\frac{10-3\pi}{12-3\pi}R
  • y_c=\frac{10-3\pi}{12-3\pi}R
Rectangular tube | axes through centroid

I_x=\frac{b h^3-(b-2t)(h-2t)^3}{12}

I_y=\frac{h b^3-(h-2t)(b-2t)^3}{12}

I_{xy}=0

Circular tube | any axis through centroid
 I_x=\frac{\pi \left(D^4-(D-2t)^4\right)}{64}
Angle | axes through corner

I_{x}=\frac{t(h^3 + b t^2 - t^3)}{3.0}

I_{y}=\frac{t(b^3 + h t^2 - t^3)}{3.0}

I_{xy}=\frac{t^2(b^2+h^2-t^2)}{4.0}

Angle | axes through centroid

I_{x}=I_{x_0}-A y_c^2

I_{y}=I_{y_0}-A x_c^2

I_{xy}=-\frac{b h t (b-t)(h-t)}{4(b+h-t)}

where:

  • I_{x_0} the moment of inertia of angle around axis x0, passing through the corner: I_{x_0}=\frac{t(h^3 + b t^2 - t^3)}{3.0}
  • I_{y_0} the moment of inertia of angle around axis y0, passing through the corner: I_{y_0}=\frac{t(b^3 + h t^2 - t^3)}{3.0}
  • A=t(b+h-t) , the area of the angle

Centroid:

  • x_c = \frac{b^2+h t - t^2}{2(b+h-t)}
  • y_c = \frac{h^2+b t - t^2}{2(b+h-t)}
Channel | axes through centroid

I_x =\frac{b h^3-(b-t_w)(h-2t_f)^3}{12}

I_y= \frac{2t_f b^3+(h -2t_f)t_w^3 }{3} - A x_c^2

I_{xy}=0

where:

  • x_c=\frac{2t_f b^2+(h-2t_f) t_w^2}{4bt_f+2h t_w-4t_f t_w}
  • A=2b t_f +h t_w -2t_f t_w
Tee | axes through centroid

I_x= \frac{t_w h^3 + (b-t_w)t_f^3}{3} - A (h-y_c)^2

I_y = \frac{t_f b^3 + (h - t_f)t_w^3}{12}

I_{xy}=0

where:

  • y_c=h-\frac{t_w h^2 + (b - t_w )t_f^2}{2A}
  • A=b t_f +t_w(h-t_f)
Double-tee | axes through centroid

I_x= \frac{b h^3 - (b-t_w)(h-2t_f)^3}{12}

I_y = \frac{2t_f b^3 + (h - 2t_f)t_w^3}{12}

I_{xy}=0

Parallel Axes Theorem
 I_{x'}=I_x+Ad^2
Axes rotation

I_u = \frac{I_x+I_y}{2} + \frac{I_x-I_y}{2} \cos{2\varphi} -I_{xy} \sin{2\varphi}

I_v = \frac{I_x+I_y}{2} - \frac{I_x-I_y}{2} \cos{2\varphi} +I_{xy} \sin{2\varphi}

I_{uv} = \frac{I_x-I_y}{2} \sin{2\varphi} +I_{xy} \cos{2\varphi}

Principal axes

I_{I,II} = \frac{I_x+I_y}{2} \pm \sqrt{\left(\frac{I_x-I_y}{2}\right)^2 + I_{xy}^2}

\tan 2\theta = -\frac{2I_{xy}}{I_x-I_y}

Jump to
-  Moments of Inertia - Reference Table

Background

Moment of inertia

The moment of inertia, or more accurately, the second moment of area, is defined as the integral over the area of a 2D shape, of the squared distance from an axis:

I=\iint_A y^2 dA

where A is the area of the shape and y the distance of any point inside area A from a given axis of rotation. From the definition, it is apparent that the moment of inertia should always have a positive value, since there is only a squared term inside the integral.

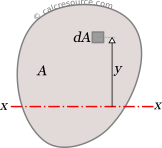
Moment of inertia around axis x-x - definition of integral terms dA and y

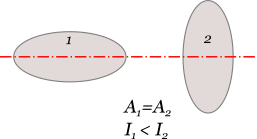
Conceptually, the second moment of area is related with the distribution of the area of the shape. Specifically, a higher moment, indicates that the shape area is distributed far from the axis. On the contrary, a lower moment indicates a more compact shape with its area distributed closer to the axis. For example, in the following figure, both shapes have equal areas, whereas, the right one, features higher second moment of area around the red colored axis, since, compared to the left one, its area is distributed quite further away from the axis.

Terminology

More than often, the term moment of inertia is used, for the second moment of area, particularly in engineering discipline. However, in physics, the moment of inertia is related to the distribution of mass around an axis and as such, it is a property of volumetric objects, unlike second moment of area, which is a property of planar areas. In practice, the following terms can be used to describe the second moment of area:

  • moment of inertia
  • area moment of inertia
  • moment of inertia of area
  • cross-sectional moment of inertia
  • moment of inertia of a beam

The second moment of area (moment of inertia) is meaningful only when an axis of rotation is defined. Often though, one may use the term "moment of inertia of circle", missing to specify an axis. In such cases, an axis passing through the centroid of the shape is probably implied.

Product of inertia

The product of inertia of a planar closed area, is defined as the integral over the area, of the product of distances from a pair of axes, x and y:

I_{xy}=\iint_A x y dA

where A is the area of the shape and x, y the distances of any point inside area A from the respective axes.

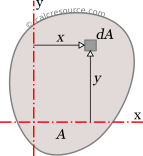
If either one of the two axes is also an axis of symmetry, then I_{xy}=0 .

Also note that unlike the second moment of area, the product of inertia may take negative values.

Further Reading

Liked this page? Share it with friends!