Jump to
Table of Contents
Share this
ADVERTISEMENT
Table of Contents
Share this
Definitions
General
The hyperbolic tangent function is defined as:
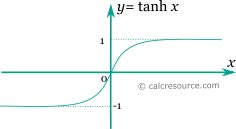
The graph of the hyperbolic tangent function is shown in the figure below. It is a monotonic function unlike the trigonometric tangent, which is periodic .
Series
All hyperbolic functions can be defined in an infinite series form. Hyperbolic tangent function can be written as:
The above series converges for . Bn denotes the n-th Bernulli number.
From the expanded form of the series it can be seen that the higher terms become insignificant, for values of x close to zero, resulting in the following quite useful approximation:
Properties
The derivative of the hyperbolic tangent function is:
The integral of the hyperbolic tangent is given by:
