ADVERTISEMENT
Definitions
General
The general exponential function has the form , where b is the base and x is the exponent which is considered variable and may take any real or complex value. Among other bases, constant e≈2.718, which is also called Euler number, is particularly useful. The so called natural exponential function , is the inverse function of natural logarithm and has the unique property that its derivative is the same function. This means that the growth rate of the function is always equal to its value. Any other exponential can be linked to the natural exponential through the following manipulation:
where
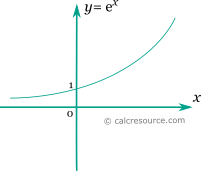
The graph of the exponential function is shown in the figure below. It is a monotonic function, that its value and its slope at 0 is 1.
Properties
The derivative of the exponential function is the same function:
The integral of the n-th power function is given by:
Identities:
