CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Square root calculator

This tool evaluates the square root of a number: . Enter the argument x below.

x =
Result:
=

Definitions

General

The square root of a number x, is a number r so that r²= x. In modern notation square root is written as or x^1/2. Since r²= (-r)², any positive number has in principle two square roots, one positive and an opposite negative one. These are usually denoted as . Depending on the application, only one of the two square roots may be associated with a physical meaning. The square root of a positive number is always a real number. The square root of 0 is 0.

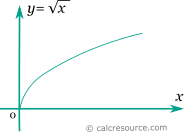
The graph of the positive square root function of non-negative numbers is shown in the figure below. It is a monotonic function with a parabolic form

Properties

The derivative of the positive square root function (x>0) is:

The integral of the positive square root function is given by:

Identities

The following formulas are valid for positive square root function:

Negative numbers

Since the square of any real number (positive or negative) is always positive, it is impossible to find a real square root of a negative number. Nevertheless, an expansion of the square root to negative numbers is meaningful for many applications. A trick is necessary in that case, employing an imaginary unit numberiwith the unique property:

Therefore, the square root of a negative number is an imaginary number: