CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Cube root calculator

This tool evaluates the cube root of a number: . Enter the argument x below.

x =
Result:
=

Definitions

General

The cube root of a number x, is a number r so that r³= x. In modern notation cube root is written as or x^1/3. Any real number has one real cube root, while any non-zero real number has two complex cube roots too. The real cube root of a positive number is always positive while the real cube root of a negative number is negative. The cube root of 0 is 0.

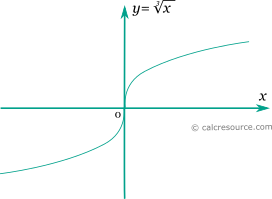
The graph of the real cube root function is shown in the figure below. It is a monotonic function with symmetry around origin.

Properties

The derivative of the cube root function is:

The integral of the cube root function is given by: