ADVERTISEMENT
Definitions
General
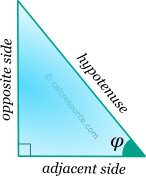
The sine function, in modern notation written as sin(x), is a trigonometric function. Trigonometric functions are commonly established as functions of angle, in the context of right triangle geometry. This way, the sine of an angle φ is defined as the ratio of the opposite side of a right triangle containing φ, divided by its hypotenuse (see figure):
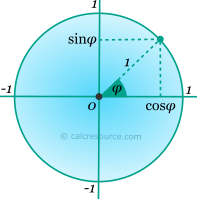
Unfortunately the above definition is limited to a range of angles between 0 and 90°. Extending that range, a convenient definition employs a unit circle (radius equal to 1). Any point of the circle, corresponds to a pair of sine and cosine values, of the angle that is contained by the horizontal positive axis and the radial segment towards that point, as shown in the figure below. Particularly, the sine is found as the coordinate on the vertical axis. The angle φ is assumed positive in counter-clockwise direction. The equivalence of the circle points, as sine and cosine pairs, is established by examining the right triangle, having as hypotenuse the radial segment towards a circumferential point (length equal to unity), and either of the axes. Angles larger than 90°, as well as negative ones, are possible, if the appropriate sign of the coordinates is respected.
The above definitions of sine function are based on a geometrical construct (right triangle or unit circle) and assume that its argument is an angle. This association to an angle is restrictive, considering the broad use of sine in mathematics, physics, engineering etc. Applications of sine, may accept any real value as argument, with any imaginable meaning given to it, or no meaning at all. In that case, x should be better measured in radians (). Thus, derivation and integration rules are more conveniently applied.
Series
All trigonometric functions can be defined in an infinite series form. Sine function can be written as:
The above series converges for any x. However, the number of terms required to converge, increases with the value of x, which makes it impractical for numerical calculations at an arbitrary range. For a limited range however (i.e. 0≤x≤π) it can be useful. From the expanded form of the series it can be seen that the higher terms become insignificant, for values of x close to zero, resulting in the following quite useful approximation:
Properties
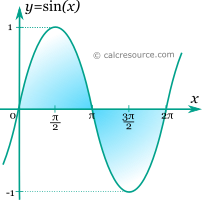
The sine function is periodic, with a period equal to 2π. Therefore:
Also the sine function changes sign at π intervals, according to the following expression:
Sine and cosine functions are associated through an argument shift equal to π/2:
The derivative of the sine function (x in radians) is the cosine:
The integral of the sine function (x in radians) is given by:
Identities
The following formulas are valid for the sine function: