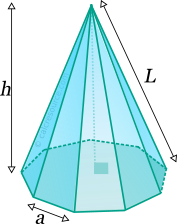
Properties of Pyramid (with polygonal base)
This tool calculates the basic geometric properties of a right pyramid, with a regular polygonal base. Enter the number of base edges 'N' and the shape dimensions 'a' and 'h' below. The calculated results will have the same units as your input. Please use consistent units for any input.
N = | |||
a = | |||
h = | |||
Geometric properties: | |||
Volume = | |||
Surface area = | |||
Base area = | |||
Lateral surface area = | |||
Lateral edge length L = | |||
Number of faces = | |||
Number of edges = | |||
Number of vertices = | |||
 |
ADVERTISEMENT
Definitions
Geometry
The pyramid is a solid object with a polygonal base and lateral faces that converge to a single point, the apex. A pyramid with triangular base is called tetrahedron and has 4 faces, 6 edges and 4 vertices, the minimums for any pyramid. With an n-sided polygon as base, the number of faces, edges and vertices of a pyramid (NF, NE, NV respectively) is given by the formulas:
where n the number of edges/vertices of the base.
The volume of a pyramid is given by the formula:
where the surface area of the base and h the height of the pyramid. For a regular polygon with n edges, the base area is given by:
where the length of an edge of the regular base polygon.
The surface area of one lateral face of the pyramid, can be found using the following formula:
where the radius of the incircle of the regular base polygon. It can be found as:
Since there are n lateral faces, the total surface area of the n base pyramid is:
The edge, that connects a base vertex with apex, has a length equal to: