Properties of a Rectangle
This tool calculates the basic geometric properties of a rectangle. Enter below the shape dimensions. The calculated results will have the same units as your input. Please use consistent units for any input.
a = | |||
b = | |||
Geometric properties: | |||
Area = | |||
Perimeter = | |||
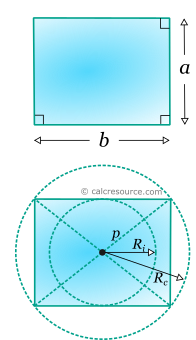
Diagonal p = | |||
Inradius Ri = | |||
Circumradius Rc = | |||
 |
ADVERTISEMENT
Definitions
Geometry
Rectangle is a quadrilateral shape with two pairs of parallel sides, that meet each other at right angles. If all sides are equal the shape is a square. The area of a rectangle is given by the formula:
where a, b the lengths of the sides.
The perimeter of a rectangle is simply the sum of the lengths of all sides:
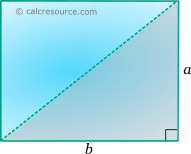
The length of the diagonal, can be expressed in terms of the length of the sides, using the Pythagorean theorem on the right triangle with the diagonal as hypotenuse:
It is not possible to inscribe a circle on a rectangle, that is tangent to all four sides, unless these are equals (shape is square). The largest circle, that can be enclosed to the shape, has a radius equal to:
On the other hand, there is a circumscribed circle (a circle that passes through all vertices) for any rectangle. Its radius is equal to:
where p the diagonal length.