Properties of a Trapezoid
This tool calculates the basic geometric properties of a trapezoid. Enter below the shape dimensions. It is not required for base α to be the bigger one. The calculated results will have the same units as your input. Please use consistent units for any input.
α = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Additional input (select which): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xc = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
yc = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lengths: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Side c = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Side d = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal p = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal q = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Angles : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ1 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ2 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ3 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ4 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
ADVERTISEMENT
Definitions
Geometry
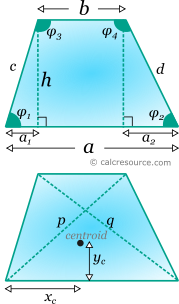
Trapezoid is a quadrilateral shape with at least two parallel sides. The definitions shown in the following figure are used:
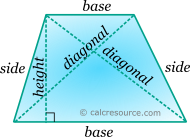
The area of a trapezoid is given by the formula:
where a, b the lengths of the two bases and h the height.
The perimeter of a trapezoid is simply the sum of the lengths of all sides:
Finding the lengths of the non parallel sides c and d, can be done if one interior angle of the trapezoid is known. Let's assume that angle φ1 is given. Using simple geometrical principles, for the right triangles, with sides c, d as hypotenuses (see figure below), the calculation of lengths c and d can by done:
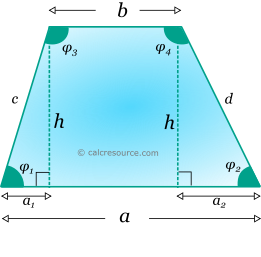
Interior angle φ3 is supplementary with φ1, since bases a and b are parallel. Therefore:
The remaining interior angles (which are also supplementary) can be found using simple geometrical principles, for the right triangle, with side d as hypotenuse:
There are many ways to find the lengths of diagonals, once the sides or the interior angles are known. Here, a solution employing the Pythagorean Theorem on the highlighted right triangle (see next figure) is presented, for diagonal p:
Similarly, the other diagonal is found as:
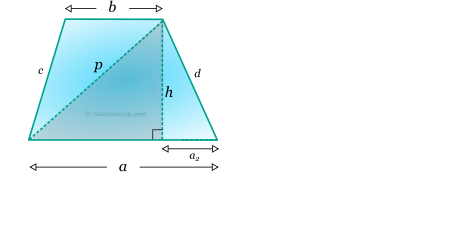
Centroid
The centroid coordinates in respect to the bottom base left vertex, xc and yc (see figure below) can be calculated using the first moments of area, of the three sub-areas A,B,C.
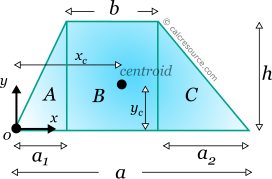
For xc, considering the first moments of area, relative to the part B middle, it is found:
where A is the area of the trapezoid.
As for the yc, considering the first moments of area relative to the bottom base, it is found:
The above formulas are valid even when α1 or α2 are negative, which occurs when the angles φ1 or φ2, are obtuse.