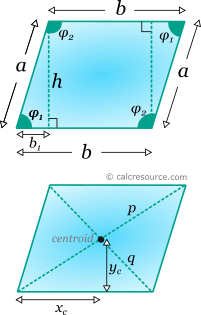
Properties of a Parallelogram
This tool calculates the basic geometric properties of a parallelogram. Enter below the shape dimensions. The calculated results will have the same units as your input. Please use consistent units for any input.
b = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Additional input (select which): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lengths: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Side α = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal p = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal q = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Angles : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ1 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ2 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Centroid: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xc = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
yc = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
ADVERTISEMENT
Definitions
Geometry
Parallelogram is a quadrilateral shape with two pairs of parallel sides. The area of a parallelogram is given by the formulas:
or
where a, b the lengths of the sides and h the height, perpendicular to b.
The perimeter of a parallelogram is simply the sum of the lengths of all sides:
The length of the left and right sides α, can be expressed in terms of the angle φ1, using the right triangle, with hypotenuse α (see figure below):
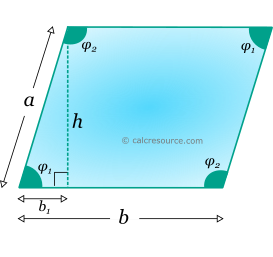
Interior angle φ2 is supplementary with φ1. Therefore:
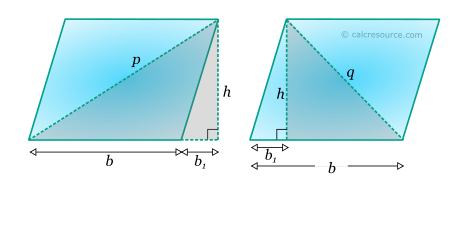
There are many ways to find the lengths of diagonals, once the sides or the interior angles are known. Here, a solution employing the Pythagorean Theorem on the highlighted right triangles (see next figure) is presented:
Similarly, the other diagonal is found as:
Centroid
The centroid of parallelogram coincides with the point where diagonals cross each other. Measuring from the left vertex of base, xc and yc distances are:
where A is the area of the trapezoid.