Jump to
Table of Contents
Share this
Properties of a Quarter-Circular Area
This tool calculates the basic geometric properties of a quarter-circular area. Enter the shape dimensions R or D below. The calculated results will have the same units as your input. Please use consistent units for any input.
R = | |||
...or | |||
D = | |||
Geometric properties: | |||
Area = | |||
Perimeter = | |||
Arc length = | |||
xc = | |||
yc = | |||
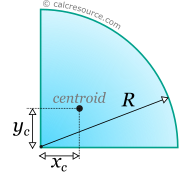 |
ADVERTISEMENT
Table of Contents
Share this
Definitions
Geometry
The area A, the perimeter P and the arc length L of a quarter-circular area, with radius R, can be found with these formulas:
The centroid (center of gravity) of the quarter-circular area is located at equal distances from the radial edges that define its border, given by the formula: