Properties of a Circular segment
This tool calculates the basic geometric properties of a circular segment. Enter below the circle radius R and either one of: central angle φ or height h or distance d. Note, that the angle φ can be greater than 180° which represents a segment bigger than the semicircle. In that case distance d is negative and height h is bigger than R. The calculated results will have the same units as your input. Please use consistent units for any input.
R = | |||
φ = | |||
...or | |||
h = | |||
...or | |||
d = | |||
Geometric properties: | |||
φ (rad) = | |||
h = | |||
d = | |||
Area = | |||
Perimeter = | |||
Arc length = | |||
Chord length = | |||
dc = | |||
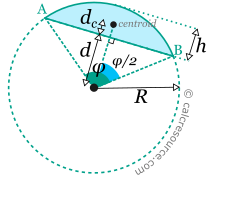 |
ADVERTISEMENT
Definitions
Geometry
For a circular segment the definitions shown in the following figure are used:
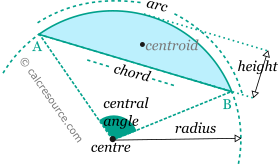
For a circular segment with radius R and central angle φ, the chord length LAB and its distance d from centre, can be found from the right triangle that occupies half of the region defined by the central angle (see next figure):
The height h of the circular segment h and its arc length L are found easily:
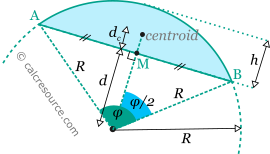
The area A and the perimeter P of a circular segment, can be found with these formulas:
where L the arc length and LAB the chord length.
The centroid (center of gravity) of the circular segment is located along the bisector of the central angle φ, and at a distances from the chord equal to:
where d the distance of the chord from the centre.