CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Cantilever beam calculator

This tool calculates the static response of cantilever beams under various loading scenarios. The tool calculates and plots diagrams for these quantities:

• reactions
• bending moments
• transverse shear forces
• deflections
• slopes

Please take in mind that the assumptions of Euler-Bernoulli beam theory are adopted, the material is elastic and the cross section is constant over the entire beam span (prismatic beam).

• Jump to the theory and formulas instead!

1	2	3	4
Structure
L =		mcmmmydftin
Optional properties, required only for deflection/slope results:
E =		PakPaMPaGPapsiksiMpsi
I =		m⁴cm⁴mm⁴ft⁴in⁴
Calculate the moment of inertia of various beam cross-sections, using our dedicated calculators.

1	2	3	4
Imposed loading:
Uniform distributed loadUniform distr. load (total)Point load at tipPoint loadPoint momentTriangular loadTrapezoidal loadTrapezoidal load (slab)Partial uniform loadPartial triangular loadPartial trapezoidal load
W =		kNNkgtlbfkip
P =		kNNkgtlbfkip
M =		kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
w =		kN/mN/mkg/mt/mlbf/ftlbf/inkip/ftlbf/m
w1 =		kN/mN/mkg/mt/mlbf/ftlbf/inkip/ftlbf/m
w1 =		kN/mN/mkg/mt/mlbf/ftlbf/inkip/ftlbf/m
w2 =		kN/mN/mkg/mt/mlbf/ftlbf/inkip/ftlbf/m
a =		mcmmmydftin
b =		mcmmmydftin
Form:	Ascending Descending
Calculate

1	2	3	4
Results:
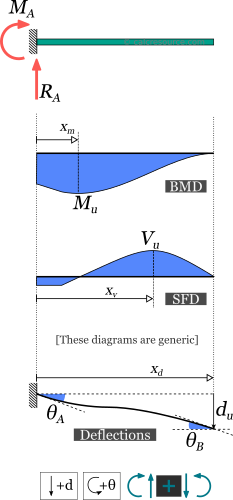
Reactions:
RA =		kNNkgtlbfkip
MA =		kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
Bending Moment:
Mu =		kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
xm =		mcmmmydftin
Transverse Shear Force:
Vu =		kNNkgtlbfkip
xv =		mcmmmydftin
Deflection:
du =		mcmmmydftin
xd =		mcmmmydftin
Slopes:
θA =		degradmrad
θB =		degradmrad

1	2	3	4
Request results at a specific point:
x =		mcmmmydftin
M(x) =		kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in
V(x) =		kNNkgtlbfkip
d(x) =		mcmmmydftin
θ(x) =		degradmrad

Theoretical background

Table of contents

Introduction

The cantilever beam is one of the most simple structures. It features only one support, at one of its ends. The support is a, so called, fixed support that inhibits all movement, including vertical or horizontal displacements as well as any rotations. The other end is unsupported, and therefore it is free to move or rotate. This free end is often called the tip of the cantilever.

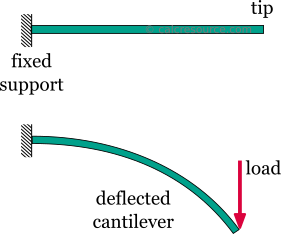
Removing the singe support or inserting an internal hinge, would render the cantilever beam into a mechanism: a body the moves without restriction in one or more directions. This is unwanted situation for a load carrying structure. As a result, the cantilever beam offers no redundancy in terms of supports. If a local failure occurs the whole structure would collapse. These type of structures, that offer no redundancy, are called critical or determinant structures. To the contrary, a structure that features more supports than required to restrict its free movements is called redundant or indeterminate structure. The cantilever beam is a determinant structure.

Assumptions

The static analysis of any load carrying structure involves the estimation of its internal forces and moments, as well as its deflections. Typically, for a plane structure, with in plane loading, the internal actions of interest are the axial force , the transverse shear force and the bending moment . For a cantilever beam that carries only transverse loads, the axial force is always zero, provided the deflections are small. Therefore it is rather common to neglect axial forces.

The calculated results in this page are based on the following assumptions:

• The material is homogeneous and isotropic (in other words its characteristics are the same in ever point and towards any direction)
• The material is linear elastic
• The loads are applied in a static manner (they do not change with time)
• The cross section is the same throughout the beam length
• The deflections are small
• Every cross-section that initially is plane and also normal to the longitudinal axis, remains plane and normal to the deflected axis too. This is the case when the cross-section height is quite smaller than the beam length (10 times or more) and also the cross-section is not multi layered (not a sandwich type section).

The last two assumptions satisfy the kinematic requirements for the Euler Bernoulli beam theory that is adopted here too.

Sign convention

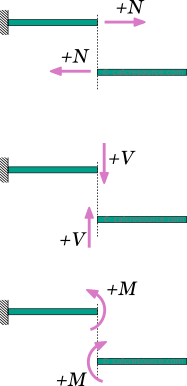
For the calculation of the internal forces and moments, at any section cut of the beam, a sign convention is necessary. The following are adopted here:

1. The axial force is considered positive when it causes tension to the part
2. The shear force is positive when it causes a clock-wise rotation of the part.
3. The bending moment is positive when it causes tension to the lower fiber of the beam and compression to the top fiber.

These rules, though not mandatory, are rather universal. A different set of rules, if followed consistently would also produce the same physical results.

Symbols

• : the material modulus of elasticity (Young's modulus)
• : the moment of inertia of the cross-section around the elastic neutral axis of bending
• : the total beam length
• : support reaction
• : deflection
• : bending moment
• : transverse shear force
• : slope

Cantilever beam with uniform distributed load

The load w is distributed throughout the cantilever span, having constant magnitude and direction. Its dimensions are force per length. The total amount of force applied to the cantilever beam is , where the beam length. Either the total force or the distributed force per length may be given, depending on the circumstances.

The following table contains the formulas describing the static response of the cantilever beam under a uniform distributed load .

Cantilever beam with uniform distributed load (UDL)
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:

Cantilever beam with point force at the tip

The force is concentrated in a single point, located at the free end of the beam. In practice however, the force may be spread over a small area, although the dimensions of this area should be substantially smaller than the cantilever length. In the close vicinity of the force application, stress concentrations are expected and as result the response predicted by the classical beam theory is maybe inaccurate. This is only a local phenomenon however. As we move away from the force location, the results become valid, by virtue of the Saint-Venant principle.

The following table contains the formulas describing the static response of the cantilever beam under a concentrated point force , imposed at the tip.

Cantilever beam with point load at tip
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:

Cantilever beam with point force at a random position

The force is concentrated in a single point, anywhere across the cantilever length. In practice however, the force may be spread over a small area. In order to consider the force as concentrated, though, the dimensions of the application area should be substantially smaller than the beam length. In the close vicinity of the force, stress concentrations are expected and as result the response predicted by the classical beam theory maybe inaccurate. This is only a local phenomenon however, and as we move away from the force location, the discrepancy of the results becomes negligible.

The following table contains the formulas describing the static response of the cantilever beam under a concentrated point force , imposed at a random distance from the fixed support.

Cantilever beam with point load at random position
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:

Cantilever beam with point moment

In this case, a moment is imposed in a single point of the beam, anywhere across the span. In practical terms, it could be a force couple, or a member in torsion, connected out of plane and perpendicular to the beam.

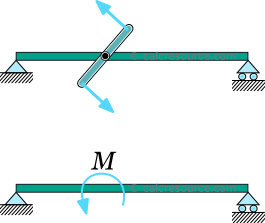
At any case, the moment application area should spread to a small length of the cantilever, so that it can be successfully idealized as a concentrated moment to a point. Although in the close vicinity the application area, the predicted results through the classical beam theory are expected to be inaccurate (due to stress concentrations and other localized effects), the predicted results become perfectly valid, when we move away, as stated by the Saint-Venant principle.

The following table contains the formulas describing the static response of the cantilever beam under a concentrated point moment , imposed at a distance from the fixed support.

Cantilever beam with point moment
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:

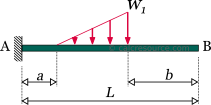
Cantilever beam with varying distributed load

The load is distributed throughout the cantilever length, having linearly varying magnitude, starting from at the fixed support, to at the free end. The dimensions of and are force per length. The total amount of force applied to the beam is , where the cantilever length.

The values of and can be freely assigned. It is not mandatory for the former to be smaller than the latter. They may take even negative values (one or both of them).

If , the formulas in the following table correspond to a triangular distributed load, with increasing magnitude (peak at the tip).

If , the formulas in the following table correspond to a triangular distributed load, with decreasing magnitude (peak at the fixed support).

The following table contains the formulas describing the static response of the cantilever beam under a varying distributed load, of trapezoidal shape.

Cantilever beam with linearly varying distributed load (trapezoidal)
Quantity	Formula
Reactions:
End slopes:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:
where:

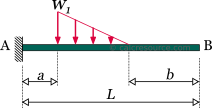
Cantilever beam with slab-type trapezoidal load distribution

This load distribution is typical for cantilever beams supporting a slab. The distribution looks like a right trapezoid, with an increasing part close to the fixed support and a constant part, with magnitude equal to , at the remaining length, up to the tip. The dimensions of are force per length. The total amount of force applied to the beam is , where, , is the cantilever length and, , is the length close to the fixed support, where the load distribution is varying (triangular).

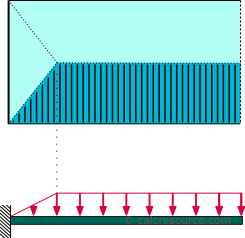
The following table contains the formulas describing the static response of the cantilever beam under a trapezoidal load distribution, due to a slab, as depicted in the schematic above.

Cantilever beam with trapezoidal load distribution (from a slab)
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:

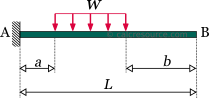
Cantilever beam with partially distributed uniform load

The load is distributed to a part of the cantilever length, with constant magnitude , while the remaining length is unloaded. The dimensions of are force per length. The total amount of force applied to the beam is , where the cantilever length and , the unloaded lengths at the left and right side of the beam, respectively.

The following table contains the formulas describing the static response of the cantilever beam under a partially distributed uniform load.

Cantilever beam with partially distributed uniform load
Quantity	Formula
Reactions:
End slopes:
Ultimate bending moment:
Ultimate shear force:
Ultimate deflection:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:
where:

Cantilever beam with partially distributed trapezoidal load

The load is distributed to a part of the cantilever length, having linearly varying magnitude from to , while the remaining length is unloaded. The dimensions of and are force per length. The total amount of force applied to the beam is , where the beam length and , the unloaded lengths at the left and right side of the beam respectively.

The values of and can be freely assigned. It is not mandatory for the former to be smaller than the latter. They may take even negative values (one or both of them).

This is the most generic case. The formulas for partially distributed uniform and triangular loads can be derived by appropriately setting the values of and . Furthermore, the respective cases for fully loaded span, can be derived by setting and to zero.

The following table contains the formulas describing the static response of the cantilever beam under a partially distributed trapezoidal load.

Cantilever beam with partially distributed linearly varying load (trapezoidal)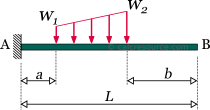
Quantity	Formula
Reactions:
End slopes:
Bending moment at x:
Shear force at x:
Deflection at x:
Slope at x:
where:

Related articles