Rotated Axes Transformation of Moments of Inertia
This tool calculates the transformed moments of inertia (second moment of area) of a planar shape, due to rotation of axes. Enter the moments of inertia Ixx, Iyy and the product of inertia Ixy, relative to a known coordinate system, as well as a rotation angle φ below (counter-clockwise positive).The calculated results will have the same units as your input. Please use consistent units for any input.
Ixx = | |||
Iyy = | |||
Ixy = | |||
φ = | |||
The transformed Moments of Inertia are: | |||
Iuu = | |||
Ivv = | |||
Iuv = | |||
 |
ADVERTISEMENT
Definitions
Transformation of Moments of Inertia due to axes rotation
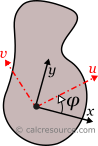
For the transformation of the moments of inertia from one system of axes x,y to another one u,v, rotated by an angle φ, the following equations are used:
where Ix, Iy the moments of inertia about the initial axes and Ixy the product of inertia. Iu, Iv and Iuv are the respective quantities for the rotated axes u,v. The product of inertia Ixy is zero, when x or y are symmetry axes.
Dimensions
The dimensions of moment of inertia (second moment of area) are .
Mass moment of inertia
In Physics the term moment of inertia has a different meaning. It is related with the mass distribution of an object (or multiple objects) about an axis. This is different from the definition usually given in Engineering disciplines (also in this page) as a property of the area of a shape, commonly a cross-section, about the axis. The term second moment of area seems more accurate in this regard.
Applications
The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure (see beam bending theory). The bending moment M applied to a cross-section is related with its moment of inertia with the following equation:
where E is the Young's modulus, a property of the material, and κ the curvature of the beam due to the applied load. Beam curvature κ describes the extent of flexure in the beam and can be expressed in terms of beam deflection w(x) along longitudinal beam axis x, as: . Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I.