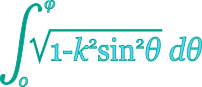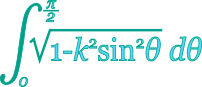Jump to
Table of Contents
Share this
ADVERTISEMENT
Table of Contents
Share this
About Elliptic Integrals of the Second Kind
Definitions
The incomplete elliptic integral of the second kind is defined as:
where k is the elliptic modulus, with . Variable is the Jacobi's amplitude.
The complete elliptic integral of the first kind is defined as:
Values
In the following table the values of the complete elliptic integral of the second kind are shown for a range of k values:
| k | E(k) |
|---|---|
| -1 | 1 |
| -0.999 | 1.004 |
| -0.99 | 1.028 |
| -0.98 | 1.05 |
| -0.97 | 1.069 |
| -0.96 | 1.087 |
| -0.95 | 1.103 |
| -0.9 | 1.172 |
| -0.8 | 1.276 |
| -0.7 | 1.356 |
| -0.6 | 1.418 |
| -0.5 | 1.467 |
| -0.4 | 1.506 |
| -0.3 | 1.535 |
| -0.2 | 1.555 |
| -0.1 | 1.567 |
| 0 | 1.571 |
| 0.1 | 1.567 |
| 0.2 | 1.555 |
| 0.3 | 1.535 |
| 0.4 | 1.506 |
| 0.5 | 1.467 |
| 0.6 | 1.418 |
| 0.7 | 1.356 |
| 0.8 | 1.276 |
| 0.9 | 1.172 |
| 0.95 | 1.103 |
| 0.96 | 1.087 |
| 0.97 | 1.069 |
| 0.98 | 1.05 |
| 0.99 | 1.028 |
| 0.999 | 1.004 |
| 1 | 1 |
In the following table the values of the incomplete elliptic integral of the second kind are shown for a range of k and φ values:
| k | E(30°,k) | E(45°,k) | E(60°,k) | E(90°,k) | E(135°,k) | E(225°,k) | E(270°,k) | E(315°,k) |
|---|---|---|---|---|---|---|---|---|
| -1 | 0.5 | 0.7071 | 0.866 | 1 | 0.7071 | -0.7071 | -1 | -0.7071 |
| -0.999 | 0.5 | 0.7073 | 0.8665 | 1.004 | 0.7073 | -0.7073 | -1.004 | -0.7073 |
| -0.99 | 0.5005 | 0.7088 | 0.8705 | 1.028 | 0.7088 | -0.7088 | -1.028 | -0.7088 |
| -0.98 | 0.501 | 0.7105 | 0.8748 | 1.05 | 0.7105 | -0.7105 | -1.05 | -0.7105 |
| -0.97 | 0.5015 | 0.7122 | 0.8791 | 1.069 | 0.7122 | -0.7122 | -1.069 | -0.7122 |
| -0.96 | 0.5019 | 0.7139 | 0.8833 | 1.087 | 0.7139 | -0.7139 | -1.087 | -0.7139 |
| -0.95 | 0.5024 | 0.7155 | 0.8873 | 1.103 | 0.7155 | -0.7155 | -1.103 | -0.7155 |
| -0.9 | 0.5046 | 0.7233 | 0.9065 | 1.172 | 0.7233 | -0.7233 | -1.172 | -0.7233 |
| -0.8 | 0.5087 | 0.7371 | 0.9395 | 1.276 | 0.7371 | -0.7371 | -1.276 | -0.7371 |
| -0.7 | 0.5123 | 0.749 | 0.9667 | 1.356 | 0.749 | -0.749 | -1.356 | -0.749 |
| -0.6 | 0.5153 | 0.7589 | 0.9892 | 1.418 | 0.7589 | -0.7589 | -1.418 | -0.7589 |
| -0.5 | 0.5179 | 0.7672 | 1.008 | 1.467 | 0.7672 | -0.7672 | -1.467 | -0.7672 |
| -0.4 | 0.52 | 0.7738 | 1.022 | 1.506 | 0.7738 | -0.7738 | -1.506 | -0.7738 |
| -0.3 | 0.5216 | 0.7789 | 1.033 | 1.535 | 0.7789 | -0.7789 | -1.535 | -0.7789 |
| -0.2 | 0.5227 | 0.7825 | 1.041 | 1.555 | 0.7825 | -0.7825 | -1.555 | -0.7825 |
| -0.1 | 0.5234 | 0.7847 | 1.046 | 1.567 | 0.7847 | -0.7847 | -1.567 | -0.7847 |
| 0 | 0.5236 | 0.7854 | 1.047 | 1.571 | 0.7854 | -0.7854 | -1.571 | -0.7854 |
| 0.1 | 0.5234 | 0.7847 | 1.046 | 1.567 | 0.7847 | -0.7847 | -1.567 | -0.7847 |
| 0.2 | 0.5227 | 0.7825 | 1.041 | 1.555 | 0.7825 | -0.7825 | -1.555 | -0.7825 |
| 0.3 | 0.5216 | 0.7789 | 1.033 | 1.535 | 0.7789 | -0.7789 | -1.535 | -0.7789 |
| 0.4 | 0.52 | 0.7738 | 1.022 | 1.506 | 0.7738 | -0.7738 | -1.506 | -0.7738 |
| 0.5 | 0.5179 | 0.7672 | 1.008 | 1.467 | 0.7672 | -0.7672 | -1.467 | -0.7672 |
| 0.6 | 0.5153 | 0.7589 | 0.9892 | 1.418 | 0.7589 | -0.7589 | -1.418 | -0.7589 |
| 0.7 | 0.5123 | 0.749 | 0.9667 | 1.356 | 0.749 | -0.749 | -1.356 | -0.749 |
| 0.8 | 0.5087 | 0.7371 | 0.9395 | 1.276 | 0.7371 | -0.7371 | -1.276 | -0.7371 |
| 0.9 | 0.5046 | 0.7233 | 0.9065 | 1.172 | 0.7233 | -0.7233 | -1.172 | -0.7233 |
| 0.95 | 0.5024 | 0.7155 | 0.8873 | 1.103 | 0.7155 | -0.7155 | -1.103 | -0.7155 |
| 0.96 | 0.5019 | 0.7139 | 0.8833 | 1.087 | 0.7139 | -0.7139 | -1.087 | -0.7139 |
| 0.97 | 0.5015 | 0.7122 | 0.8791 | 1.069 | 0.7122 | -0.7122 | -1.069 | -0.7122 |
| 0.98 | 0.501 | 0.7105 | 0.8748 | 1.05 | 0.7105 | -0.7105 | -1.05 | -0.7105 |
| 0.99 | 0.5005 | 0.7088 | 0.8705 | 1.028 | 0.7088 | -0.7088 | -1.028 | -0.7088 |
| 0.999 | 0.5 | 0.7073 | 0.8665 | 1.004 | 0.7073 | -0.7073 | -1.004 | -0.7073 |
| 1 | 0.5 | 0.7071 | 0.866 | 1 | 0.7071 | -0.7071 | -1 | -0.7071 |
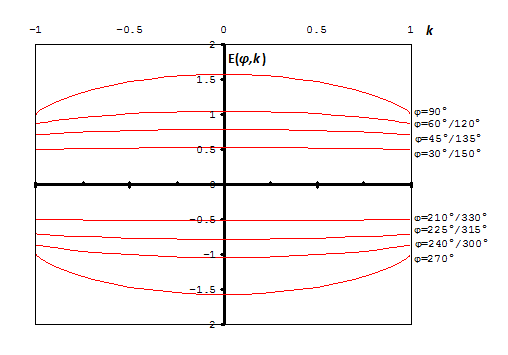
The xy plots of the incomplete integral of the second kind for various values of amplitude φ are depicted in the following figure: