Jump to
-  Calculator
-  About Carlson's symmetric form of Elliptic Integrals
Table of Contents
-  Calculator
-  About Carlson's symmetric form of Elliptic Integrals
-  Definitions
Share this
See also
Evaluate Elliptic Integral of the first kind
Evaluate Elliptic Integral of the second kind
Evaluate Elliptic Integral of the third kind
All evaluation tools

Carlson's Elliptic Integrals

- By Dr. Minas E. Lemonis, PhD - Updated: March 3, 2019
Home > Evaluation > Carlson's form of Elliptic Integrals

This tool evaluates the Carlson's symmetric form of elliptic integrals: RF(x,y,z), RC(x,y), RD(x,y,z) and RJ(x,y,z,p). Arguments x, y, z should be generally non-negative, but more restrictions apply. Argument p should be non-zero. Enter the arguments below.

x =
y =
z =
p =
icon

icon

Result:
RF (x,y,z) =
RC (x,y) =
RD (x,y,z) =
RJ (x,y,z,p) =
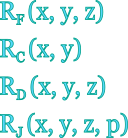shape details

ADVERTISEMENT

Table of Contents
-  Calculator
-  About Carlson's symmetric form of Elliptic Integrals
-  Definitions
Share this

About Carlson's symmetric form of Elliptic Integrals

Definitions

The Carlson's symmetric form of the elliptic integral of the first kind is defined as:

R_F(x,y,z) = \frac{1}{2}\int_{0}^{\infty}\frac{dt}{\sqrt{(t+x)(t+y)(t+z)}}

The Carlson's degenerate elliptic integral of the first kind, with y=z, is defined as:

R_C(x,y) = R_F(x,y,y) = \frac{1}{2}\int_{0}^{\infty}\frac{dt}{(t+y)\sqrt{(t+x)}}

The Carlson's symmetric form of the elliptic integral of the second kind is defined as:

R_D(x,y,z) = \frac{3}{2}\int_{0}^{\infty}\frac{dt}{(t+z)\sqrt{(t+x)(t+y)(t+z)}}

The Carlson's symmetric form of the elliptic integral of the third kind is defined as:

R_J(x,y,z,p) = \frac{3}{2}\int_{0}^{\infty}\frac{dt}{(t+p)\sqrt{(t+x)(t+y)(t+z)}}

See also
Evaluate Elliptic Integral of the first kind
Evaluate Elliptic Integral of the second kind
Evaluate Elliptic Integral of the third kind
All evaluation tools