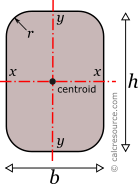
Properties of Rounded Rectangle Cross-Section
This tool calculates the properties of a rectangular cross-section with rounded corners. Enter the shape dimensions 'b', 'h' and 'r' below. The calculated results will have the same units as your input. Please use consistent units for any input.
b = | |||
h = | |||
r = | |||
Geometric properties: | |||
Area = | |||
Perimeter = | |||
Properties related to x-x axis: | |||
Ix = | |||
Sx = | |||
Zx = | |||
Rgx = | |||
ADVERTISEMENT | |||
Properties related to y-y axis: | |||
Iy = | |||
Sy = | |||
Zy = | |||
Rgy = | |||
Other properties: | |||
Iz = | |||
 |
ADVERTISEMENT
Definitions
Geometry
The area A and the perimeter P of a rounded rectangle cross-section, having sides of length b, h and round corner radius r, are found with the next formulas:
Moment of Inertia
The moment of inertia (second moment of area) of a rectangle in respect to an axis x-x passing through its centroid, parallel to its base b, is given by the following expression:
where b is the base width, and specifically the dimension parallel to the axis, and h is the height (more specifically, the dimension perpendicular to the axis). For the rounded rectangle cross-section, the contribution of the cut-out corner areas should be removed from the above moment of inertia. Considering there are 4 of them, at equal distances from axis x, the moment of inertia of the rounded rectangle is:
where the moment of inertia of the cut-out corner around the x-x axis. Finding this, is more straightforward if the cut-out shape is considered as the difference between a square with side r and a quarter circle, as demonstrated in the next figure and described by the formula:
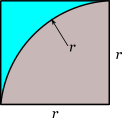
The moment of inertia of the square around x axis, , can be found, considering the distance of its centroid from the axis is: . Taking advantage of the parallel axis theorem we find:
The moment of inertia of the quarter circle around x axis, , can be found, considering the distance of its centroid from the axis is: and its second moment of area around its own centroid: . Taking advantage of the parallel axis theorem we find:
Finally, we can calculate the whole section moment of inertia around x-x as:
Similarly, the moment of inertia (second moment of area) of a rounded rectangle with respect to a centroidal axis y-y perpendicular to its base, can be found, by alternating dimensions b and h, in the last equation:
The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. The bending moment M applied to a cross-section is related with its moment of inertia with the following equation:
where E is the Young's modulus, a property of the material, and κ the curvature of the beam due to the applied load. Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I.
The polar moment of inertia, describes the rigidity of a cross-section against torsional moment, likewise the planar moments of inertia described above, are related to flexural bending. The calculation of the polar moment of inertia Iz about an axis z-z (perpendicular to the section), can be done with the Perpendicular Axes Theorem:
where the Ix and Iy are the moments of inertia about axes x-x and y-y that are mutually perpendicular with z-z and meet at a common origin.
The dimensions of moment of inertia are .
Elastic section modulus
The elastic section modulus Sx of any cross section about axis x-x (centroidal), describes the response of the section under elastic flexural bending. It is defined as:
where Ix the moment of inertia of the section about x-x axis and Y the distance from centroid of a section point (aka fiber, typically the most distant one), measured perpendicularly to x-x axis. Application of the above formula to the rounded rectangle cross-section gives its elastic section modulus about x-x axis:
Similarly, for the section modulus Sy, relative to y-y axis, which happens to be symmetry axis too, the above definitions are written as:

If a bending moment Mx is applied on axis x-x, the section will respond with normal stresses, varying linearly with the distance from the neutral axis (which under elastic regime coincides to the centroidal x-x axis). Along neutral axis the stresses are zero. Absolute maximum σ will occur at the most distant fiber, with magnitude given by the formula:
From the last equation, the section modulus can be considered for flexural bending, a property analogous to cross-sectional A, for axial loading. For the latter, the normal stress is F/A.
The dimensions of section modulus are .
Plastic section modulus
The plastic section modulus is similar to the elastic one, but defined with the assumption of full plastic yielding of the cross section due to flexural bending. In that case the whole section is divided in two parts, one in tension and one in compression, each under uniform stress field. For materials with equal tensile and compressive yield stresses, this leads to the division of the section into two equal areas, At in tension and Ac in compression, separated by the neutral axis. The axis is called plastic neutral axis, and for non-symmetric sections, isn't the same with the elastic neutral axis (which again is the centroidal one). The plastic section modulus is given by the general formula:
where Yc is the distance of the centroid of the compressive area Ac from the plastic neutral axis and Yt the respective distance of the centroid of the tensile area At. By definition, the terms and represent the first moments of area of the compression and tension zones, and , respectively therefore the plastic modulus can be written as:
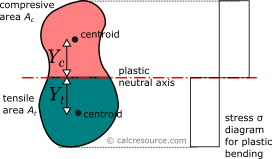
For the case of a rounded rectangle, the plastic neutral axis passes through centroid, dividing the whole area into two equal parts, and furthermore . The calculation of the plastic modulus can be easily formulated:
where:
For the above calculation, the cut-out corner area was considered as the difference of a square with side r and a quarter circle with the same radius.
Similarly, the plastic modulus of a rounded rectangle with respect to a centroidal axis y-y, perpendicular to its base, can be found, by alternating dimensions b and h, to the last formulas.
Radius of gyration
Radius of gyration Rg of a cross-section, relative to an axis, is given by the formula:
where I the moment of inertia of the cross-section about the same axis and A its area. The dimensions of radius of gyration are . It describes how far from centroid the area is distributed. Small radius indicates a more compact cross-section.