CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Natural logarithm calculator

This tool evaluates the natural logarithm of a number: . Enter the argument x below.

x =
Result:
=

Definitions

General

The natural logarithm of a number x, is a power p so that e^p= x, where e is a mathematical constant, approximately equal to 2.718. In modern notation natural logarithm is written as or . Any positive real number has a natural logarithm. The natural logarithm of 1 is 0, while the natural logarithm of 0 approaches negative infinity.

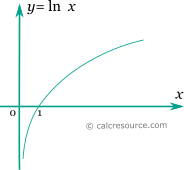
The graph of the natural logarithm function is shown in the figure below. It is a monotonic function.

Properties

The derivative of the natural logarithm function is:

The integral of the natural logarithm function is given by: