Newton - Pound Force converter / N-lbf
Enter the force in either of the next two fields and get it converted instantly, from Newton to pound force (N to Lbf), or the reversely, from pound force to Newton (Lbf to N).
Newtons [N] : | |||
Pounds force [Lbf]: | |||
 |
Conversion Formulas
1 Newton ≈ 0.22481 pound force
1 Pound force ≈ 4.4482 Newton
ADVERTISEMENT
Definitions
Table of contents
The pound force unit
The pound force (symbolized lbf or lb-f) is a unit of force according to the Imperial and US customary systems of units. Often it is called just pounds, especially when the surrounding context implies a quantity of force. Even though pound-force is closely related to the respective pound, which is a unit of mass, it is considered best practice to use the pound-force name.
Pound force is defined as the force of gravity on the earth's surface upon a mass equal to one avoirdupois pound. Its equivalence to the respective metric unit, the Newton [N] is: 1 lbf = 4.4482216152605 N. The above definition depends on the earth's gravitational acceleration g, which varies from place to place, but is conventionally averaged to g ≈ 32.1740 ft/s2, at sea level.

Pound force and other units
The relationship between pound force (lbf) and other units of force are shown in the following table:
| Unit | Symbol | [Lbf] |
|---|---|---|
| Newton | N | 0.22481 |
| Kilonewton | kN | 224.81 |
| Meganewton | MN | 224809 |
| Giganewton | GN | 2.2481 108 |
| Millinewton | mN | 2.2481 10-4 |
| Kilogram-force | kp | 2.2046 |
| Poundal | pdl | 0.031081 |
A quick example how to use the above table is given here. Assuming, you need to find the relationship between Kilo-newton (kN) and pound force (lbf), the following equation is derived from the table: 1 KN = 222.81 lbf.
The Newton unit
Newton [N] is a unit of force according to the SI system of units. It is a derived unit, based on the kilogram [Kg], a unit of mass, the metre [m], a unit of length and the second [s], a unit of time. It is defined as the force required to accelerate a mass equal to 1 Kg by 1 m/s2, according to the Newton's second law of motion:
where F the force, m the mass and a the acceleration.
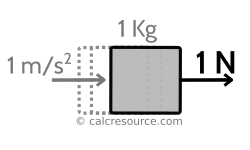
Newton and other units
The relationship between Newton and other units of force is shown in the following table:
| Unit | Symbol | [N] |
|---|---|---|
| Kilonewton | kN | 1000 |
| Meganewton | MN | 106 |
| Giganewton | GN | 109 |
| Millinewton | mN | 10-3 |
| Pound force | lbf | 4.448222 |
| Kilogram force | kp | 9.80665 |
| Poundal | pdl | 0.138255 |
A quick guide how to use the above table is given here. Assuming, you need to find the relationship between Meganewtons (MN) and Newtons (N), the following equation is derived from the table: 1MN = 106 N.
How to convert pound force to Newtons (lbf to N)
- Multiply force in lbf with 4.4482216152605
- The result is the force in N
For example to convert 100 lbf to N we have: 100x4.4482216152605 ≈ 444.8 N
How to convert Newtons to pound force (N to lbf)
- Divide force in N by 4.4482216152605
- The result is the force in lbf
For example to convert 1000 N to lbf we have: 1000/4.4482216152605 ≈ 224.8 lbf
Weight and mass
Do you find it difficult to distinguish between mass and weight? In everyday practice these two quantities are sometimes confused as identical, and most of times, we are used to overcome it, without severe implications. But, when the time comes to perform a calculation, employing either weights or masses, or both of them, it is important to distinguish between the two and to correlate one with the other.
Mass is a fundamental property of matter, that practically describes the resistance of an object to change its current rate of movement. The more mass an object has, the harder it should be to make it accelerate, or turn, or force it to stop, if it is already moving. Also, the mass describes how strongly an object can pull other objects through gravity and similarly, how strongly it is affected by other objects gravitational fields. A given object has the same mass, either on Earth's surface, or on Mars or wherever it is placed in the universe (theory of relativity aside).
Weight is a force. It is the force that Earth's gravity applies to an object with a given mass. Therefore, it is a quantity related to the mass, but it is also related to gravitational field around the object, which varies from one location to another. Therefore, a given object would have different weights if placed at sea level or on top of a mountain. Most scales actually measure weight, instead of mass. As a result, a bag of apples, weighed by the same scale, will be slightly heavier at sea level, where the gravity is stronger, compared to a ski resort in Alps, where gravity is weaker, potentially saving you a penny or two. That is unless, the store owner, takes measures and calibrates the scale appropriately for his altitude. This example demonstrates that the weight of an object is not a universal property, even though we are used to treat it so, for convenience in our everyday transactions.
We can easily derive the weight of an object, knowing its mass and vice-versa. From the Newton's 2nd law of motion, the force exerted to an object is directly proportional to its mass and its acceleration. In that case, the acceleration is the earth's gravitational acceleration g. As indicated above, the value of g depends on the altitude above sea level as well on the geographic latitude. Using its conventional value, which is g ≈ 9.80665 m/s2 (corresponding to 45° latitude, at sea-level) we find that 1 kg of mass is pulled by earth, with a force equal to:
- W = 1 kg x 9.80665 m/s2 = 9.80665 N
Reversely, 1 Newton is the weight at sea level of a mass equal to:
- m = 1 N / 9.80665 m/s2 = 0.10197 kg
In imperial units, the conventional value of Earth's gravity is g ≈ 32.1740 ft/s2. Thus, the weight of a mass equal to 1 pound is found as:
- W = 1 lb x 32.1740 ft/s2 = 32.174 lb.ft/s2
By definition though, the weight of 1 lb of mass, at sea level, is exactly 1 lbf. Therefore, from the last expression we get the equivalence of lbf to lb.ft/s2, which is:
- 1 lbf = 32.174 lb.ft/s2
And reversely:
- 1 lb.ft/s2 = 1 / 32.174 lb.ft/s2 ≈ 0.03108 lbf
Conversion table from Newton to pound-force (N to lbf)
In the following table some typical force values in N are converted to lbf:
| [N] | [lbf] |
|---|---|
| 1 | 0.2248 |
| 5 | 1.124 |
| 10 | 2.248 |
| 20 | 4.496 |
| 30 | 6.744 |
| 40 | 8.992 |
| 50 | 11.24 |
| 70 | 15.74 |
| 90 | 20.23 |
| 100 | 22.48 |
| 150 | 33.72 |
| 200 | 44.96 |
| 300 | 67.44 |
| 400 | 89.92 |
| 500 | 112.4 |
| 600 | 134.9 |
| 700 | 157.4 |
| 800 | 179.8 |
| 900 | 202.3 |
| 1000 | 224.8 |
| 2000 | 449.6 |
| 3000 | 674.4 |
Conversion table from pound force to Newton (lbf to N)
In the following table some typical force values in lbf are converted to N:
| [lbf] | [N] |
|---|---|
| 0.25 | 1.112 |
| 0.5 | 2.224 |
| 0.75 | 3.336 |
| 1 | 4.448 |
| 2 | 8.896 |
| 3 | 13.34 |
| 4 | 17.79 |
| 5 | 22.24 |
| 6 | 26.69 |
| 7 | 31.14 |
| 8 | 35.59 |
| 9 | 40.03 |
| 10 | 44.48 |
| 12 | 53.38 |
| 15 | 66.72 |
| 20 | 88.96 |
| 25 | 111.2 |
| 30 | 133.4 |
| 35 | 155.7 |
| 40 | 177.9 |
| 45 | 200.2 |
| 50 | 222.4 |
| 60 | 266.9 |
| 70 | 311.4 |
| 80 | 355.9 |
| 90 | 400.3 |
| 100 | 444.8 |
| 150 | 667.2 |
| 200 | 889.6 |