Properties of Prism (with polygonal base)
This tool calculates the basic geometric properties of a right prism, with a regular polygonal base. Enter the number of base edges 'N' and the shape dimensions 'a' and 'h' below. The calculated results will have the same units as your input. Please use consistent units for any input.
N = | |||
a = | |||
h = |
Geometric properties: | |||
Volume = | |||
Surface area = | |||
Base area = | |||
Lateral surface area = | |||
Number of faces = | |||
Number of edges = | |||
Number of vertices = | |||
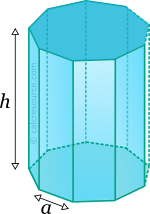 |
ADVERTISEMENT
Definitions
Geometry
The prism is a solid object enclosed by two parallel planar polygonal bases and a lateral prismatic surface. Cube is a prism while cylinder can be considered a prism with infinite number of lateral faces. With a polygonal base, having n sides/vertices, the number of faces, edges and vertices (NF, NE, NV respectively) is given by the formulas:
The volume of a prism is given by the formula:
where the surface area of the base and h the height of the prism. For a regular polygon with n edges, the base area is given by:
where the length of an edge of the base regular polygon.
The surface area of one lateral face of the prism, is equal to:
Since there are n lateral faces and two bases, the total surface area of the n base prism is: