Properties of Pyramid
This tool calculates the basic geometric properties of a right pyramid, with a square base. Enter the shape dimensions 'a' and 'h' below. The calculated results will have the same units as your input. Please use consistent units for any input.
a = | |||
h = | |||
Geometric properties: | |||
Volume = | |||
Surface area = | |||
Base area = | |||
Lateral surface area = | |||
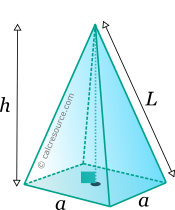
Lateral edge length L = | |||
 |
ADVERTISEMENT
Definitions
Geometry
The pyramid is a solid object with a polygonal base and side faces that converge to a single point, the apex. Typically the most recognizable pyramid is the one with square base. This type is examined in this page. A square based pyramid, has 5 faces, 8 edges and 5 vertices.
The volume of a square based pyramid is given by the formula:
where a the length of a base side and h the height of the pyramid. This formula is derived from the following general expression, that covers all pyramids, with any polygonal base, and also the cone:
where the base area.
The surface area of one side face of the square based pyramid, can be found using the following formula:
Since there are four side faces and the area of the square base is equal to , the total surface area of the square based pyramid is:
The edge, that connects a base vertex with apex, has a length equal to: