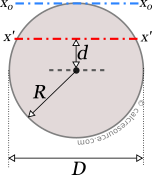
Moment of Inertia of a Circle
This tool calculates the moment of inertia I (second moment of area) of a circle. Enter the radius 'R' or the diameter 'D' below. The calculated result will have the same units as your input. Please use consistent units for any input.
R = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
or... | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Select axis: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area A = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT
Background
Moment of inertia of circle
The moment of inertia of circle with respect to any axis passing through its centre, is given by the following expression:
where R is the radius of the circle.
Expressed in terms of the circle diameter D, the above equation is equivalent to:
Units
The above equations for the moment of inertia of circle, reveal that the latter is analogous to the fourth power of circle radius or diameter. Since those are lengths, one can expect that the units of moment of inertia should be of the type: . In fact, this is true for the moment of inertia of any shape, not just the circle. By definition, the moment of inertia is the second moment of area, in other words the integral sum of cross-sectional area times the square distance from the axis of rotation, hence its dimensions are .
Typical units for the moment of inertia, in the imperial system of measurements are:
- in4,
- ft4
Typical units for the moment of inertia, in metric, are:
- mm4,
- cm4,
- m4
Definition
The second moment of area of any planar, closed shape is given by the following integral:
where A is the area of the shape and y the distance of any point inside area A from a given axis of rotation.
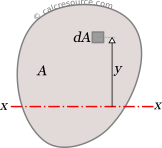
From this definition it becomes clear that the moment of inertia is not a property of the shape alone but is always related to an axis of rotation. Often though, one may use the term "moment of inertia of circle", missing to specify an axis. Depending on the context, an axis passing through the center may be implied, however, for more complex shapes it is not guaranteed that the implied axis would be obvious.
From the definition also, it is also apparent that the moment of inertia should always have a positive value, since there is only a squared term inside the integral.
Finding the equation for the moment of inertia of a circle
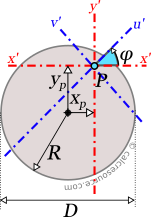
Using the above definition, which applies for any closed shape, we will try to reach to the final equation for the moment of inertia of circle, around an axis x passing through its center. First we must define the coordinate system. Since we have a circular area, the Cartesian x,y system is not the best option. Instead we choose a polar system, with its pole O coinciding with circle center, and its polar axis L coinciding with the axis of rotation x , as depicted in the figure below. The independent variables are r and φ. Specifically, for any point of the plane, r is the distance from pole and φ is the angle from the polar axis L, measured in counter-clockwise direction.
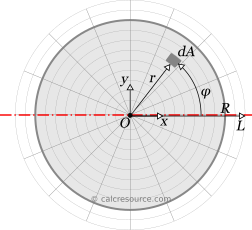
With this coordinate system, the differential area dA now becomes: , where ds is the differential arc length for differential angle dφ.
Furthermore, the area, enclosed by the circle, should have these boundaries:
Moreover, the coordinate y of any point, can be expressed in terms of the polar coordinates r and φ. To do so, we consider for the arbitrary point P (see figure) the blue colored right triangle and using simple trigonometry we find:
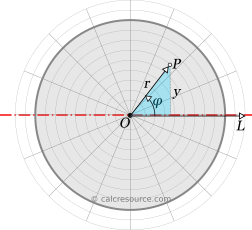
Therefore, the definite integral for the moment of inertia of the circle should be written as:
First, we integrate over variable φ.
We take advantage of the trigonometric identity: and we calculate the integral inside the parentheses like this:
Substituting to the expression of Ix, we now have to integrate over variable r:
Parallel Axes Theorem
The moment of inertia of any shape, around an arbitrary, non centroidal axis, can be found if its moment of inertia around a centroidal axis, parallel to the first one, is known. The so-called Parallel Axes Theorem is given by the following equation:
where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape.
For example, if we need the moment of inertia of a circle around an axis, that is tangent to the circumference, we make these considerations:
- d=R
Applying the Parallel Axes Theorem we find:
It turns out that the new moment of inertia is drastically increased compared to the centroidal one. This is a more general characteristic. Since the distance from centroid is squared, it affects the moment of inertia much more than the area A.
Mass moment of inertia
In Physics the term moment of inertia has a different meaning. It is related with the mass distribution of an object (or multiple objects) about an axis. This is different from the definition usually given in Engineering disciplines (also in this page) as a property of the area of a shape, commonly a cross-section, about the axis. The term second moment of area seems more accurate in this regard.
Applications
The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure (see beam bending theory). The bending moment M applied to a cross-section is related with its moment of inertia with the following equation:
where E is the Young's modulus, a property of the material, and κ the curvature of the beam due to the applied load. Beam curvature κ describes the extent of flexure in the beam and can be expressed in terms of beam deflection w(x) along longitudinal beam axis x, as: . Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I.