Properties of a Rhombus
This tool calculates the basic geometric properties of a rhombus (also called diamond shape). Enter below the shape dimensions. The calculated results will have the same units as your input. Please use consistent units for any input.
Known data: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lengths: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Side α = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal p = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagonal q = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Height h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Angles : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ1 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ2 = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
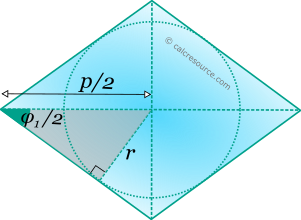
Inscribed circle: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Radius r = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
ADVERTISEMENT
Definitions
Geometry
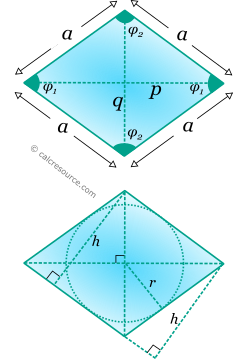
Rhombus (also called diamond shape) is a quadrilateral shape with all four sides equal. Pairs of opposite sides are parallel and pairs of opposite angles are equal. Therefore rhombus is also a parallelogram and features all parallelogram properties. It differs from square in its interior angles which are not all equal and 90°.
The area of a rhombus is given by the formulas:
where a the length of the sides and h the height, perpendicular to a side from an opposite vertex. Height h can be found, using any of the right triangles, with hypotenuse α shown in figure below:
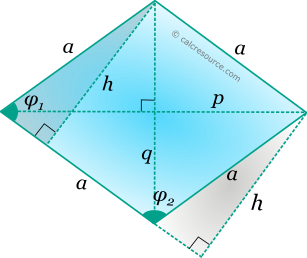
Interior angle φ2is supplementary with φ1. Therefore:
Diagonals p and q of rhombus are mutually bisecting each other, and they also bisect the interior angles φ1and φ2. Diagonals can be expressed in terms of side lengths and interior angles as:
The perimeter of a parallelogram is simply the sum of the lengths of all sides:
The radius of the inscribed circle, can be determined, using the right triangle, with hypotenuse (see figure below):