CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Hyperbolic Secant Calculator

This tool evaluates the hyperbolic secant of a number: sech(x). Enter the argument x below.

x =
Result:
sech(x) =

Definitions

General

The hyperbolic secant function is defined as:

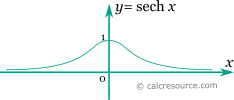
The graph of the hyperbolic secant function is shown in the figure below.

Series

All hyperbolic functions can be defined in an infinite series form. Hyperbolic secant function can be written as:

The above series converges for . E_n denotes the n-th Euler number .

Properties

The derivative of the hyperbolic secant function is:

The integral of the hyperbolic secant is given by:

Identities