CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Hyperbolic cosine calculator

This tool evaluates the hyperbolic cosine of a number: cosh(x). Enter the argument x below.

x =
Result:
cosh(x) =

Definitions

General

The hyperbolic cosine function is defined as:

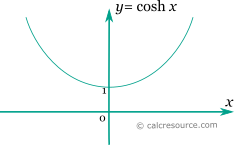
The graph of the hyperbolic cosine function is shown in the figure below. It is a monotonic function, unlike the trigonometric cosine, which is periodic.

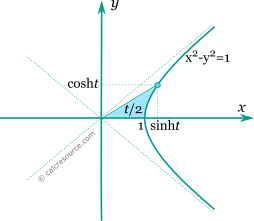
The points form the right wing of an equilateral hyperbola (see figure below), just like the trigonometric cosine, sine pairs form a circle.

The points form the right wing of an equilateral hyperbola (see figure below), just like the trigonometric cosine, sine pairs form a circle. Parameter t is the half area between the hyperbola, the x-axis and a ray from origin to the point.

Series

All hyperbolic functions can be defined in an infinite series form. Hyperbolic cosine function can be written as:

Properties

The derivative of the hyperbolic cosine function is the hyperbolic sine:

The integral of the hyperbolic cosine is given by:

Identities