ADVERTISEMENT
Definitions
General
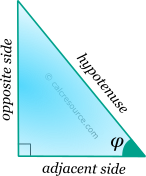
The cosine function, in modern notation written as cos(x), is a trigonometric function. Trigonometric functions are commonly established as functions of angle, in the context of right triangle geometry. This way, the cosine of an angle φ is defined as the ratio of the adjacent side of a right triangle containing φ, divided by its hypotenuse (see figure):
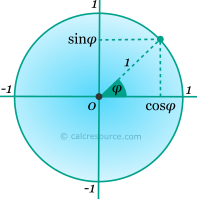
Unfortunately the above definition is limited to a range of angles between 0 and 90°. Extending that range, a convenient definition employs a unit circle (radius equal to 1). Any point of the circle, corresponds to a pair of sine and cosine values, of the angle that is contained by the horizontal positive axis and the radial segment towards that point, as shown in the figure below. Particularly, the cosine is found as the coordinate on the horizontal axis. The angle φ is assumed positive in counter-clockwise direction. The equivalence of the circle points, as sine and cosine pairs, is established by examining the right triangle, having as hypotenuse the radial segment towards a circumferential point (length equal to unity), and either of the axes. Angles larger than 90°, as well as negative ones, are possible, if the appropriate sign of the coordinates is respected.
The above definitions of cosine function are based on a geometrical construct (right triangle or unit circle) and assume that its argument is an angle. This association to an angle is restrictive, considering the broad use of trigonometric functions in mathematics, physics, engineering etc. Applications may accept any real value as argument, with any imaginable meaning given to it, or no meaning at all. In that case, x should be better measured in radians (). Thus, derivation and integration rules are more conveniently applied.
Series
All trigonometric functions can be defined in an infinite series form. Cosine function can be written as:
The above series converges for any x. However, the number of terms required to converge, increases with the value of x, which makes it impractical for numerical calculations at an arbitrary range. For a limited range however (i.e. 0≤x≤π) it can be useful.
Properties
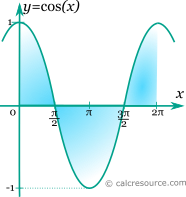
The cosine function is periodic, with a period equal to 2π. Therefore:
Also the cosine function changes sign at π intervals, according to the following expression:
Sine and cosine functions are associated through an argument shift equal to π/2:
The derivative of the cosine function (x in radians) is:
The integral of the cosine function (x in radians) is given by:
Identities
The following formulas are valid for the cosine function: