CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Trigonometric cosecant calculator

This tool evaluates the cosecant of a number: csc(x). Enter the argument x, in radians or degrees, below.

x =		deg rad
Result:
csc(x) =
Also, at same x:
sec(x) =
sin(x) =

Definitions

General

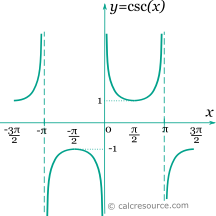
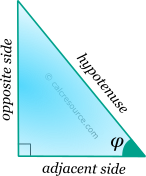
The cosecant function, in modern notation written as csc(x), is a trigonometric function. Trigonometric functions are commonly established as functions of angle, in the context of right triangle geometry. This way, the cosecant of an angle φ is defined as the ratio of the hypotenuse divided by the opposite side of a right triangle containing φ (see figure):

The above definition of cosecant function assumes that its argument is an angle. This association to an angle is restrictive, considering the broad use of trigonometric functions in mathematics, physics, engineering etc. Applications may accept any real value as argument, with any imaginable meaning given to it, or no meaning at all. In that case, x should be better measured in radians (). Thus, derivation and integration rules are more conveniently applied.

Series

All trigonometric functions can be defined in an infinite series form. Cosecant function can be written as:

The above series converges for . B_n denotes the n-th Bernulli number .

Properties

The cosecant function is periodic, with a period equal to 2π. Therefore:

Coecant is the reciprocal of sine:

The derivative of the cosecant function (x in radians) is given by the following expressions:

The integral of the cosecant function (x in radians) is given by: