Jump to
-  Properties
-  Formulas

HEA sections table

- By Dr. Minas E. Lemonis, PhD - Updated: April 9, 2024
Home > Resources > HEA section tables

In this page the properties of the European HE-A steel sections are tabulated (also known as IPBl). HE-A profiles are wide-flange, double-tees with parallel flanges.

Looking for a specific HEA section?
Table configuration:
Design Code:
Steel:
E =
fy =
HEA section dimensions and y/z axis orientation
HEA properties table
Units:
DimensionsWeightGeometryDetailingMajor AxisMinor AxisShearTorsion/Warping
Profile h b t_f t_w r G A P Surface AreaSurface Area d h_i c e I_y W_{el,y} W_{pl,y} W_{ep,y} i_y I_z W_{el,z} W_{pl,z} W_{ep,z} i_z A_{vz} A_{vy} I_t I_w
(*) W_{ep} is provided only for Eurocode 3 (2022) class 3 sections
HEA strength and classification table
No safety factors applied to the strength calculations
Units:
Major Axis BendingMinor Axis BendingClassification for local buckling
ProfileMomentShear M_{el} M_{pl} MomentShear M_{el} M_{pl} Flexure-MajorFlexure-MinorCompression
---
(**) Class 4 sections or shear buckling calculations for Eurocode 3 are not yet supported
List of symbols
h :
the overall height of the section
b :
the overall width of the section (=width of the flanges)
t_f :
the flange thickness
t_w :
the web thickness
r :
the radius of the fillet
G :
weight of the section (per length)
A :
area of the cross-section
P :
perimeter of the cross-section
d :
the parallel length of the web (net distance between flanges minus the fillets)
h_i :
distance between flanges (including the fillets)
c :
parallel length of the half-flange (fillet excluded)
e :
cantilever length of the half-flange (fillet included)
I_y, I_z :
moment of inertia (2nd moment of area) around major axis (y) or minor axis (z), respectively
W_{el,y}, W_{el,z} :
section modulus (elastic) around major axis (y) or minor axis (z), respectively
W_{pl,y}, W_{pl,z} :
plastic section modulus around major axis (y) or minor axis (z), respectively
W_{ep,y}, W_{ep,z} :
elasto-plastic section modulus [2] around major axis (y) or minor axis (z), respectively
i_y, i_z :
radius of gyration (i.e \sqrt{I/A} ) around major axis (y) or minor axis (z), respectively
A_{vz} :
shear area of the section for load parallel to web (axis z)
A_{vy} :
shear area of the section for load parallel to flanges (axis y)
I_t :
torsional constant
I_w :
warping constant
M_{el} :
elastic moment (the moment causing the edge fibers to yield)
M_{pl} :
plastic moment (moment for fully plastified section)
Statistical information
Here, a visualization of some key properties of the HEA sections are given as a function of either sectional height h or sectional weight G .
Steel:
Design Code:
Share this
Table of Contents
-  Properties
-  Formulas
-  Geometrical properties
-  Weight
-  Mechanical properties
-  Loading parallel to web
-  Loading parallel to flanges
-  Moment of inertia
-  Radius of gyration
-  Section modulus
-  Plastic section modulus
-  Shear area
-  Torsional loading
-  Torsion constant
-  Warping constant
-  References
See also
Moments of Inertia Table
Properties of I/H section
All Cross Section tools
All Moment of Inertia tools

ADVERTISEMENT

Share this
See also
Moments of Inertia Table
Properties of I/H section
All Cross Section tools
All Moment of Inertia tools

Formulas

Table of contents

-  Geometrical properties
-  Weight
-  Mechanical properties
-  References

icon

Since HE-A profiles are European, the nomenclature of Eurocode 3 is adopted herein for the naming of axes, mechanical properties etc.

Geometrical properties

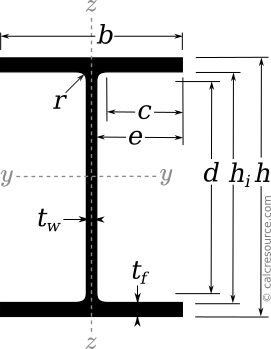
HE-A sections are European, wide-flange, double-tee profiles with parallel flange edges. Their dimensions are standardized in EURONORM 53-62, using the following five properties:

  • h the height of the section
  • b the width of the flanges
  • t_w the web thickness
  • t_f the flange thickness
  • r the fillet radius

These definitions are shown in the following figure.

Basic dimensions of HEA section
Basic dimensions of HE-A sections

Other geometrical properties can be derived from the five basic dimensions. For instance, the following properties provide some measurements of the section that can be useful for detailing purposes:

  • h_i=h-2t_f the clear distance between flanges
  • d=h-2t_f-2r the straight segment of the web
  • e=\frac{b-t_w}{2} the length from the flange edge to the web
  • c=\frac{b-t_w}{2}-r the straight segment of the flange (one half of it)

These are illustrated in the following figure:

Additional geometrical properties of the HEA section
Additional geometrical properties of HE-A sections

The section area and the perimeter of any HE-A section can be formulated as:

  • Area: A=2bt_f + h_it_w + (4-\pi)r^2
  • Perimeter: P=2h+2b + 2(\pi - 4)r

Weight

The weight of any beam with a section that doesn't change along its length (aka prismatic beam) is determined by the section area A and the density of the material. Considering carbon steel, which has a density equal to 7850 kg/m3 (or equivalently 0.2836 lbf/in3), the weight per length of a HEA beam, with section area A , is found as:

  • G = A(\text{m}^2) \times 7850 \text{ kg/m}^3 (the result in kg/m)

or:

  • G = A(\text{cm}^2) \times 0.7850 (the result in kg/m)

or:

  • G = A(\text{in}^2) \times 0.2836 \text{ lbf/in}^3 (the result in lbf/in)

Mechanical properties

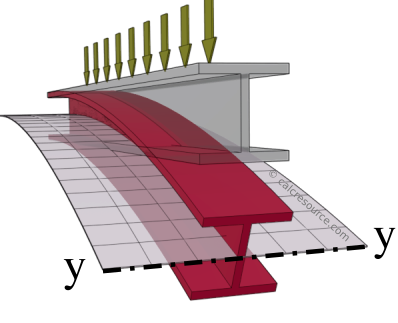
Loading parallel to web

Mechanical properties related to the transverse loading of a beam are necessarily defined around an axis of bending. This in term, depends on the direction of loading. Loading parallel to the web results in bending around axis y, also called major axis. Accordingly, all mechanical properties related to bending around y, are marked with index y. Such a case is illustrated in the following drawing.

H beam with loading parallel to web, showing deformed shape and axis of bending (major axis)
Loading parallel to web causes major axis (y) bending

Loading parallel to flanges

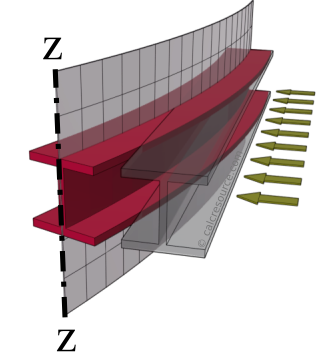
Loading parallel to the flanges results in bending around axis z, also called minor axis. Accordingly, all mechanical properties related to bending around z, are marked with index z. Such a case is illustrated in the following drawing.

H beam with loading parallel to flanges, showing deformed shape and axis of bending (minor axis)
Loading parallel to flanges causes minor axis (z) bending
Moment of inertia

The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. For a HEA section, it can be calculated with the following formulas, for loading parallel to web (i.e. bending around y) or parallel to flanges (i.e. bending around z), respectively:

I_y=\frac{bh^3}{12} - \frac{eh_i^3}{6} + (1-\frac{\pi}{4})h_i^2r^2 - ({10\over3}-\pi)h_i r^3+ (4-\frac{5\pi}{4})r^4

I_z=\frac{t_f b^3}{6} + (4-\frac{5\pi}{4})r^4 +(1-\frac{\pi}{4})t_w^2r^2 + ({10\over3}-\pi)t_w r^3 +\frac{h_i t_w^3}{12}

Radius of gyration

The radius of gyration is property that describes how far from the axis the area of the section is distributed. It is given by the following two formulas, for the major axis (y) and minor axis (z), respectively:

i_y = \sqrt{\frac{I_y}{A}}

i_z = \sqrt{\frac{I_z}{A}}

Section modulus

The section modulus of a section is typically used for the calculation of its strength in bending, assuming linear elastic conditions (for this reason also called elastic section modulus). It is directly related to the moment of inertia. For a symmetric section around the axis of bending - (HEA is symmetric around both major and minor axis), it can be calculated with the next two formulas, for loading parallel to web (i.e. bending around y) or parallel to flanges (i.e. bending around z), respectively:

W_{el,y} = \frac{2 I_y}{h}

W_{el,y} = \frac{2 I_z}{b}

Plastic section modulus

The plastic modulus of a section is typically used for the calculation of its strength in bending, assuming fully plastic conditions. For a HEA section, it can be calculated with the following formulas, the first one for loading parallel to web (i.e. bending around y) and the second for loading parallel to flanges (i.e. bending around z), respectively:

W_{pl,y}=\frac{b h^2}{4} - \frac{e h_i^2}{2} + (2-{\pi\over2})h_i r^2 - ({10\over3}-\pi)r^3

W_{pl,z}=\frac{t_f b^2}{2} + (2-{\pi\over2})t_w r^2 + ({10\over3}-\pi)r^3 + \frac{h_i t_w^2}{4}

Shear area

The shear area of a section is typically used for the calculation its strength against shear. For loading parallel to the web, shear area is roughly the area of the web (different approximations are given in building codes):

  • A_{vz}=A - 2 b t_f + (t_w+r)t_f \nless \eta h_i t_w , according to Eurocode 3 (2005, 2022). Conservatively, \eta can be 1.
  • A_{vz}=h t_w , according to ANSI/AISC 360-16 (2016):

For loading parallel to the flanges, shear area is the combined area of the two flanges:

  • A_{vy}=2bt_f

Torsional loading

HEA sections are open sections and under torsional moments they develop both St Venant torsion and warping.

Torsion constant

The torsion constant is related to the rigidity of the section under St. Venant torsion. Closed formed solutions are not available however, and its calculation is typically performed either through numerical methods or using empirical expressions. Here, the formula in Kraus & Kindmann (2009) is adopted:

I_t = {2\over3} \left(b-b_r\right) t_f^3 + {1\over 3}\left(h-2d_r\right)t_w^3 + \alpha b_r d_r^3

where:

b_r=t_w+\frac{r^2}{d_r-t_f}\frac{4-\pi}{2}

d_r=\frac{\left(t_f+r\right)^2 +\left(r+t_w/4\right)t_w}{2r+t_f}

\alpha=0.46 -0.5\left({d_r\over b_r}-1.15\right)^2

Warping constant

The warping constant for HEA sections is calculated by the formula:

I_w = \frac{t_f b^3}{24}\left(h-t_f\right)^2

References

Euronorm 53-62 (1962), Breedflensbalken met parallele flenzen; Publications Office of the European Union.

AISC (2016), Specification for structural steel buildings ANSI/AISC 360-16; American Institute of Steel Construction: Chicago, USA

Eurocode 3, EN1993-1, (2005), Design of steel structures - Part 1-1: General Rules and Rules for Buildings; CEN, Brussels, Belgium.

Eurocode 3, EN1993-1, (2022), Design of steel structures - Part 1-1: General Rules and Rules for Buildings; CEN, Brussels, Belgium.

Kraus, M., & Kindmann, R. (2009). St. Venants Torsion Constant of Hot Rolled Steel Profiles and Position of the Shear Centre. In Proceedings of 11th Nordic Steel Construction Conference (NSCC), Malmö, Sweden (pp. 454-461).

Share this
See also
Moments of Inertia Table
Properties of I/H section
All Cross Section tools
All Moment of Inertia tools