Jump to
Jump to
Share this
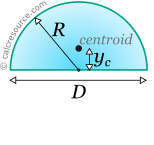
Properties of a Semi-Circular Area
This tool calculates the basic geometric properties of a semi-circular area. Enter the shape dimensions R or D below. The calculated results will have the same units as your input. Please use consistent units for any input.
R = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
...or | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Radius = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diameter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Arc length = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
yc = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Jump to
Share this
Definitions
Geometry
The area A, the perimeter P and the arc length L of a semi-circular area, with radius R, can be found with these formulas:
\[ \begin{split} A & = \frac{\pi R^2}{2} \\ P & = \left(\pi+2\right) R \\ L & = \pi R \end{split} \]
The centroid (center of gravity) of the semi-circular area is located at a distance from the diameter that defines its border, given by the formula:
\[ y_c = \frac{4 r}{3 \pi} \]